平面内模拟万有引力
研究性学习报告
一、研究背景
在高中物理必修二中,我们学习了牛顿运动定律和万有引力定律的有关内容,领略了宇宙中无穷的奥秘。
虽然在现阶段的物理界中,牛顿定律的理论基础已经被爱因斯坦的广义相对论所取代。但它在大多数应用中仍然被用作重力效应的经典近似。只有在需要极端精确的时候,或者在处理非常强大的引力场的时候,比如那些在极其密集的物体上,或者在非常近的距离时,才需要相对论。
介于一种学以致用的精神,考虑到我们的计算机基本水平,我们产生了对于模拟万有引力的极大兴趣。
二、研究方法
1.物理原理
在这个模型中,我们将每个星球抽象为一个有质量的质点,运用经典力学中的万有引力定律和质点运动规律进行运算。
(1).万有引力定律
定义:任意两个质点由通过连心线方向上的力相互吸引。该吸引力的大小与它们的质量乘积成正比,与它们距离的平方成反比,与两物体的化学本质或物理状态以及中介物质无关。
矢量表达式:
(2).质点运动规律
设质量为m的质点Q,在F1,F2,…,FN诸力的作用下运动。若以a表示质点的加速度,则由牛顿第二定律有:
又因为加速度a是位移的二阶导数,可得:
式中r为质点的矢径,这是矢量形式的质点运动微分方程。
在物理中,速度、位移、加速度均为有方向的矢量;对于计算机中,二维矢量的方向不便于表示,此时联想到所学的正交分解法,通过三角函数将有方向的向量分别分解到两个垂直的方向上。这样就便于计算机进行存储和计算。
在直角坐标轴上投影,得:
2.计算机原理
(1).工具及模块
- Python3.6及以上版本
- Python第三方库模块pygame用以可视化表现
- Python第三方库模块easygui用以与用户进行可视化交互操作
- Python第三方库模块matplotlib用以记录基本数据和进行数学操作
(2).原理
在物理中,速度、位移、加速度均为有方向的矢量;对于计算机中,二维矢量的方向不便于表示,此时联想到所学的正交分解法,通过三角函数将有方向的向量分别分解到两个垂直的方向上。这样就便于计算机进行存储和计算。
数据结构与存储
介于这一点,对于进行星球部分的数据结构如下:
1 | class plt(object): |
在这个类中,
*.status存储在屏幕上绘制星球所需的图片*.rect存储星球图片在渲染过程中的大小*.pos存储星球的坐标位置,是类似于(200,200)的一个二元向量结构,分别表示在X轴和Y轴方向上的数值,以下的加速度、速度等都是如此*.acc存储星球的加速度,二元向量结构*.vel存储星球的速度,二元向量结构*.mass存储星球的质量*.recordline记录星球的轨迹,*.recordspeed记录星球的速度
以上,便实现了对于星球数据的基本存储。
计算
1 | def cal(a, b): |
在这个函数中,传入两个刚刚新建的plt类变量。通过计算两者横纵坐标之差,根据勾股定理计算距离,接着计算出两者万有引力大小。根据横纵坐标之差,夹角的sin值和cos值进一步将万有引力分解到X轴和Y轴上,函数最终返回值是两者的万有引力分解到X轴方向和Y轴方向上的二元向量。
渲染循环
具体请看程序内注释
1 | while (1 == 1): |
有部分游戏暂停时的交互、更新记录等函数未完整给出。
交互
pygame模块中有关于按键事件的监测,easygui模块中可以轻松调用一些简单的可交互式窗口,便于用户进行最基本的操作,如修改星球、添加星球、修改基本参数、查看数据记录等。
具体代码实现部分过长,可以去开源托管网站(下一章节有提及)查看。
三、研究成果
整个项目现以完成,并在以下两个平台开源:
simulate-gravity: 模拟引力 - Gitee.com https://gitee.com/wzcwzc0/simulate-gravity/tree/main/
wzcwzc05/simulate-gravity https://github.com/wzcwzc05/simulate-gravity/tree/main
1.安装及运行项目
(1).Windows
从官方网站https://www.python.org/downloads/下载Python安装包。
注意安装时勾选Add to Path,自动加入环境变量。
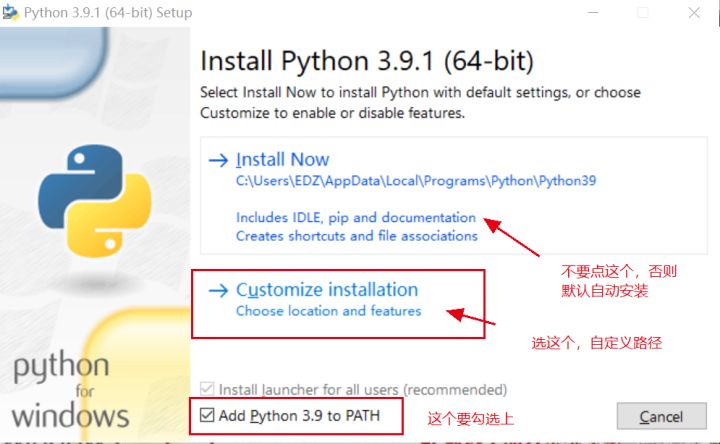
并进行完整安装(包含pip包管理器)
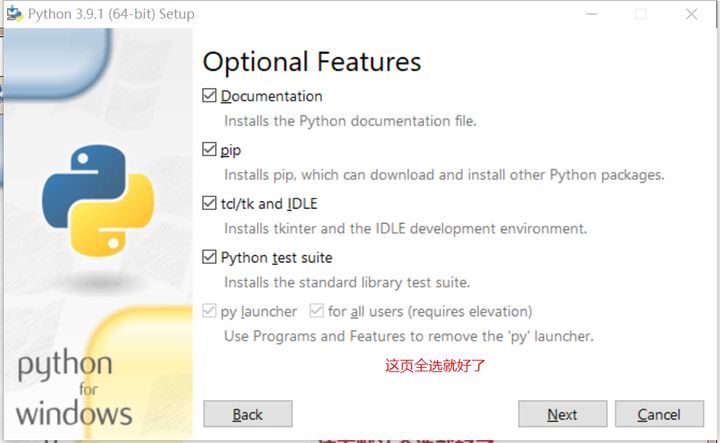
TIPS: Windows 7及以下系统不再支持Python3.9及以上版本。
出现如下两张图即为成功:
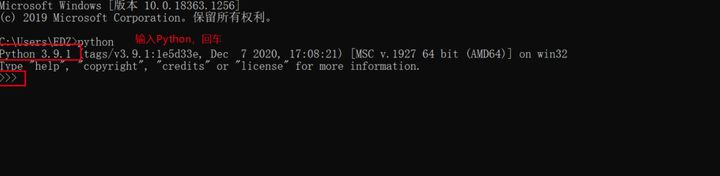
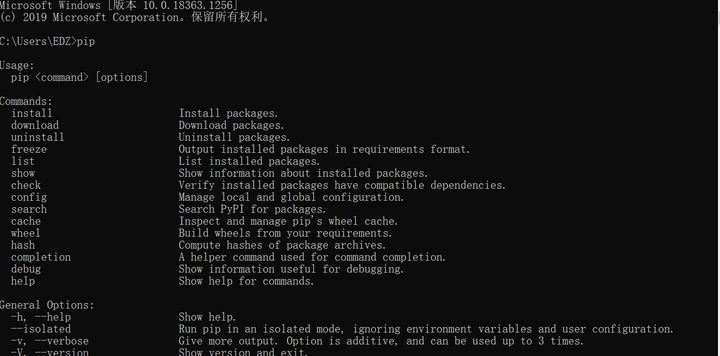
下一步使用pip包管理器安装项目依赖的第三方库:
1 | pip install pygame easygui matplotlib |
如果在中途出现大量错误信息,有可能是pip源在国外,导致下载失败,可以使用清华源:
1 | pip install pygame easygui matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple |
出现以下的环境即为安装成功:

此时来到项目目录下执行python main.py即可运行项目
(2).Linux
Linux往往安装系统时自带Python,不过还是要检查一下python版本:

可以看到版本是3.10.2,只要版本在3.6以上皆可以兼容。
下一步使用pip包管理器安装项目依赖的第三方库:
1 | pip install pygame easygui matplotlib |
如果在中途出现大量错误信息,有可能是pip源在国外,导致下载失败,可以使用清华源:
1 | pip install pygame easygui matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple |
出现以下的环境即为安装成功:

此时来到项目目录下执行python main.py即可运行项目
2.演示图
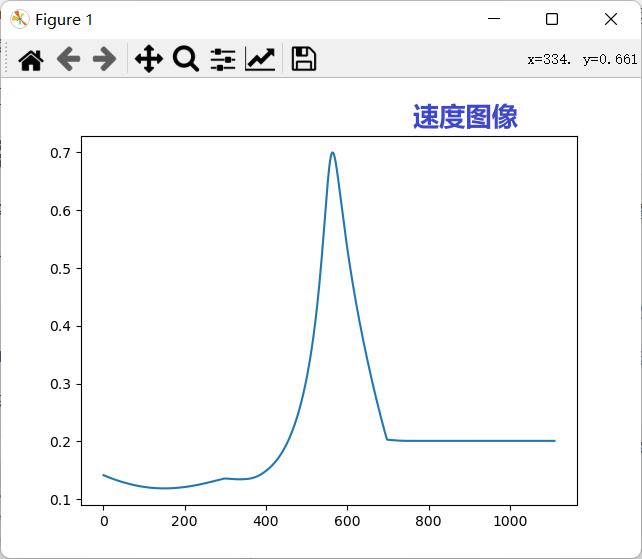
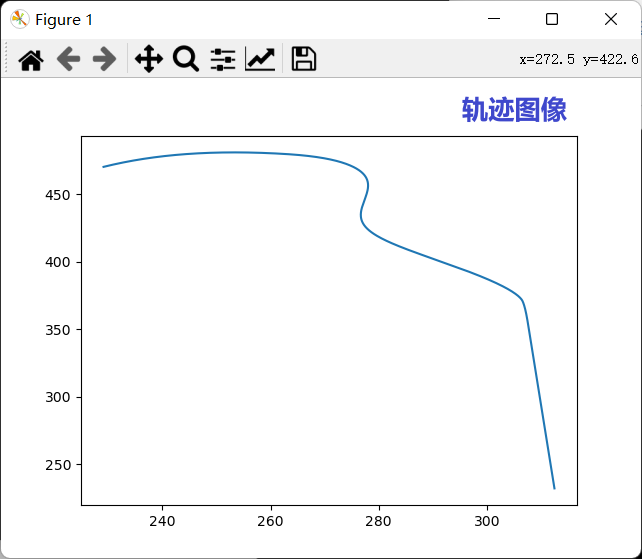
四、示例
下面演示模拟构建一个存在一个质量为10000的中心天体的恒星系。
首先左键暂停,添加中心天体:
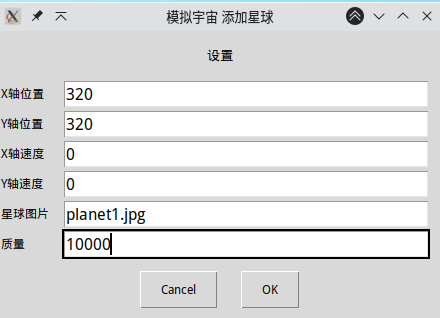
计算质量为1的行星在距离为200时进行匀速圆周运动所需的线速度:
添加行星:
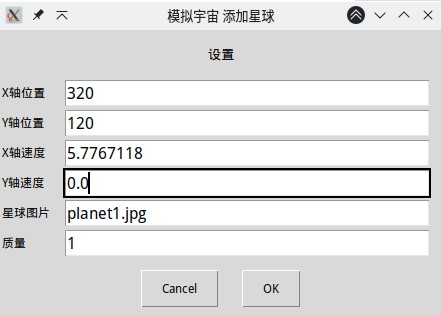
最终结果:
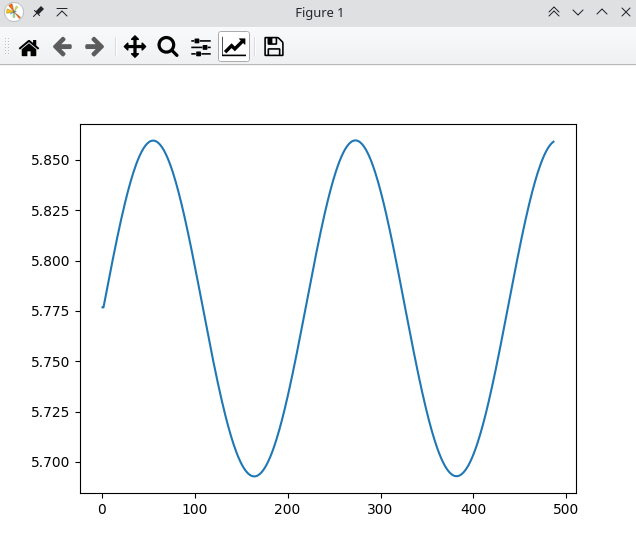
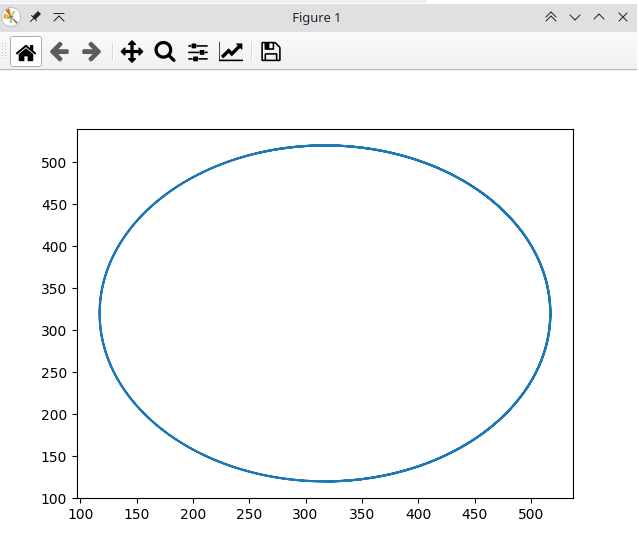
速度误差范围在可接受范围内,可近似认为是匀速圆周运动。
五、改进及其建议
虽然程序的大体已经完成,基本功能已经得到实现,但依旧存在与用户交互效果不够好等问题。
在核心原理上,万有引力定律属于经典力学范畴,对于广义相对论存在一定的不足,后期可以考虑使用引力场代替力的计算。
同时在两个星球距离过近时,并未加入碰撞或撕裂等判断,导致一些不合理现象的产生,后期可以加入碰撞或撕裂的判断。








